Here’s the headline in Nature: “Peculiar pattern found in ‘random’ prime numbers“, an article which opens “Two mathematicians have found a strange pattern in prime numbers — showing that the numbers are not distributed as randomly as theorists often assume”.
The author, Evelyn Lamb, probably means by “distributed as randomly” distributed uniformly. Now that phrase “distributed uniformly” is tricky. In the interpretation I think she has in mind, it means laying out all primes—or perhaps all those after 5; the primes 1, 2, 3, and 5 are special cases—the ending digits should be equally represented among 1, 3, 7, and 9. (Obviously, numbers ending in 2, 4, 5, 6, and 8 all have divisors of 2 or 5 and aren’t prime.)
This infinite-uniformity might be true, but that is no guarantee that any finite collection of primes shares the same property. And, in fact, most finite collections don’t. Here’s one: 117 (it’s still a collection). Not too uniform, that. But since the number of primes is infinite, we can collect infinite subsequences of primes and check their properties.
Before that, what about distributed? What a tricky word! It’s appropriate in a way. Some thing, or possibly things, caused the universe to be in such a way that prime numbers have the properties they do. What was this thing (or things)? On that subject, mathematicians (and scientists) are silent. In any case, some thing caused the primes to be distributed in the fashion they are. Our knowledge of the distribution is not the knowledge of the cause of the distribution.
Epistemology is not ontology, yet the two are often mixed up. Lamb goes on to say, “number theorists find it useful to treat the primes as a ‘pseudorandom’ sequence, as if it were created by a random-number generator.” Random means unknown and is thus always a misnomer when used in phrases like “random-number generator”. These are deterministic algorithms with known inputs and fixed, known outputs. Yet they’re called “random”. Why? Because, their writers turn a blind eye to the algorithm used and ask how people who don’t know the algorithm see the sequence: can these strangers find any way to predict the sequence, even imperfectly? If not, then the sequence is called (unfortunately) “random”. If they can, then it isn’t.
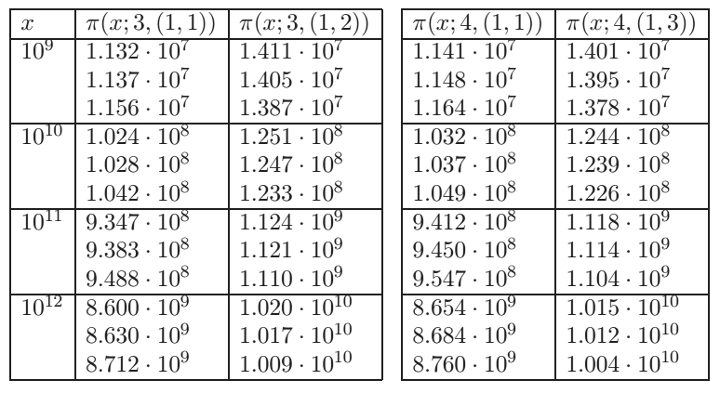
The paper in question is “Unexpected biases in the distribution of consecutive primes” by Robert J. Lemke Oliver and Kannan Soundararajan. It opens by remarking that Chebyshev had long ago noted that in the first million primes, a certain property “seem[s] to be slightly preferred”. The property was found in only 499,829 of the first million and not 500,000 as uniformity would suggest. Or as “randomness” would suggest if by that word we meant non-predictabile.
The authors modified the property and found that this modification showed departures from uniformity for a finite sequence (the first hundred million). Of course, departures in finite subsequences, as we saw above, may or may not be interesting. What makes the authors’ work important is that they prove, given modest assumptions, that the departures from uniformity hold in infinite sequences (for some but not all the properties they checked). (The modest assumptions are not known to be true, but everybody believes them. Also interesting is that this paper is not peer-reviewed, yet its argument still is treated worthy of discussion: amen to that.)
The authors say:
Despite the lack of understanding of [the certainty property], any model based on the randomness of the primes would suggest strongly that every permissible pattern of r consecutive primes appears roughly equally often;
This equates “randomness” with uniformity. Understand that unpredictability has degrees. If all you know is that some proposition is “normally distributed” (with fixed parameters), then you cannot predict the precise value of that proposition, but you do know that some intervals have greater probabilities than others. This is a departure from uniformity and is, in a weak sense, more predictable.
That same kind of weak predictability is what has been found for some properties of sequences of primes. Lamb summarizes “it would seem that this is because gaps between primes of multiples of 10 (20, 30, 100 and so on) are disfavoured.”
That “disfavoured” is an interesting choice of words. It acknowledges that whatever it was that caused primes to have these newly discovered (or any) properties liked, for whatever reason, the departure from uniformity. These are words describing the actions of intellect—and they are not out of place. For some intelligence had to create. It cannot have been “randomness”, which is not a physical thing, which created “randomness.”